Discrete Mathematics

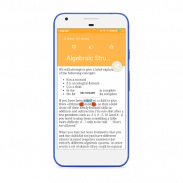
It is designed swipe based for engineering student of all streams to learn discrete mathematics. It almost cover all important topics which are covered chapter wise.

Chapter 1 Set Theory, Relation, Function, Theorem Proving Techniques

1. Set Theory

2. countable and uncountable sets

3. Venn Diagrams

4. proofs of some general identities on sets Relation in Venn Diagrams

5. types of relation

6. composition of relations

7. Equivalence relation

8. Partial ordering relation

9. one-to-one Function

10. into and onto function

11. Inverse Functions

12. Pigeonhole Principle

Chapter 2 Algebraic Structures

1. Algebraic structures

2. Abelian group

3. Subgroups

4. cyclic group

5. Homomorphism and isomorphism of Groups

6. Rings and Fields

Chapter 3 Propositional Logic

1. Proposition

2. Conditional Statements

3. Truth Tables of Compound Propositions

4. Logic and Bit Operations

5. PROPOSITIONAL EQUIVALENCES

6. Logical Equivalences

7. Constructing New Logical Equivalences

8. Predicates

9. Quantifiers

10. Infinite States and Infinite State Transitions

11. Finite state machines as language recognizers

Chapter 4 Graph Theory

1. Introduction of graphs

2. Basic Terms of Graph Theory

3. Planer graphs

4. multigraph

5. isomorphic Graph

6. paths, cycles, trails, and circuits

7. Shortest paths

8. Eulerian and Hamiltonian paths and circuits

9. Graph coloring

10. chromatic number

11. Homomorphism and isomorphism of Groups

Chapter 5 Posets, Hasse Diagram and Lattices

1. Posets, Hasse Diagram

2. ordered set

3. Hasse diagrams

4. isomorphic ordered set

5. well ordered set

6. properties of Lattices

7. bounded and complemented lattices

8. Combinatorics

9. Permutation and combination

10. Binomial Theorem

11. Introduction to Recurrence Relation and Recursive algorithms

12. Linear recurrence relations with constant coefficients

13. Homogeneous solutions

</div> <div jsname="WJz9Hc" style="display:none">Se golpe está diseñado en base a estudiante de ingeniería de todos los flujos de aprender matemáticas discretas. Casi cubre todos temas importantes que están cubiertos capítulo sabio.

Capítulo 1 Teoría de Conjuntos, Relaciones, funciones, técnicas Teorema Demostrando

1. Teoría de Conjuntos

2. Los conjuntos contables e incontables

3. Los diagramas de Venn

4. pruebas de algunas identidades generales sobre conjuntos Relación de diagramas de Venn

5. tipos de relación

6. Composición de las relaciones

7. relación de equivalencia

8. relación de orden parcial

9. uno-a-una función

10. en y sobre la función

11. Funciones inversas

12. principio del palomar

Capítulo 2 Estructuras algebraicas

1. Estructuras algebraicas

2. grupo abeliano

3. Subgrupos

4. grupo cíclico

5. homomorfismo y isomorfismo de grupos

6. Anillos y campos

Capítulo 3 Lógica Proposicional

1. Proposición

2. Las declaraciones condicionales

3. Tablas de verdad de proposiciones compuestas

4. Lógica y Bit Operaciones

5. EQUIVALENCIAS PROPOSICIONALES

6. Equivalencias lógicas

7. La construcción de nuevas Equivalencias lógicas

8. Los predicados

9. Los cuantificadores

10. Los Estados infinito e infinito de transiciones de estado

11. máquinas de estados finitos como reconocedores de lenguaje

Capítulo 4 Teoría de Grafos

1. Introducción de gráficos

2. Condiciones básicas de la Teoría de Grafos

3. Los gráficos Planer

4. multigrafo

5. Gráfico isomorfo

6. caminos, ciclos, senderos y circuitos

7. caminos cortos

8. Euler y hamiltonianos caminos y circuitos

9. Gráfico colorear

10. Número cromática

11. homomorfismo y isomorfismo de grupos

Capítulo 5 Posets, el diagrama de Hasse y Rejas

1. Posets, el diagrama de Hasse

2. conjunto ordenado

3. Los diagramas de Hasse

4. isomorfo conjunto ordenado

5. bien conjunto ordenado

6. propiedades de Rejas

7. celosías delimitadas y complementadas

8. Combinatoria

9. Permutación y combinación

10. teorema binomial

11. Introducción a la recurrencia algoritmos de relaciones y recursivos

12. relaciones de recurrencia lineales con coeficientes constantes

13. soluciones homogéneas</div> <div class="show-more-end">